N & NP

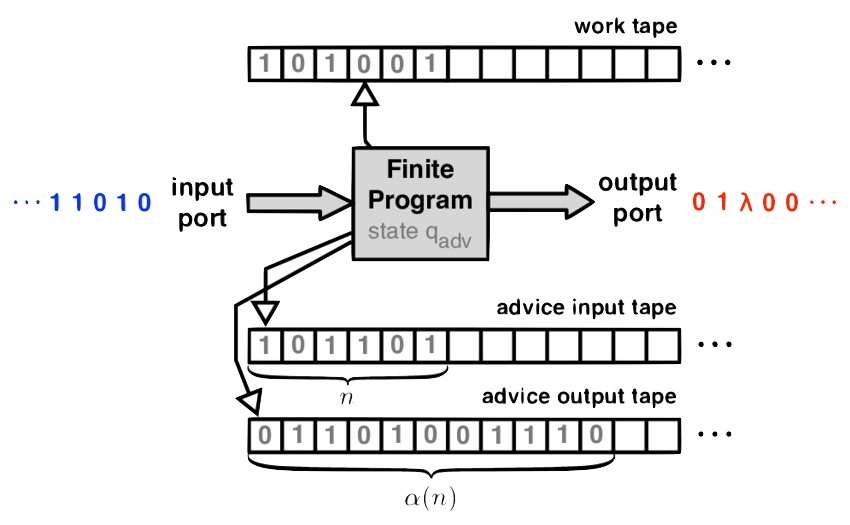
P问题

对于该问题的所有输入，都可以在多项式时间内得到结果。从语言(language)的角度，使用确定性图灵机(deterministic turing machine)可做如下定义

\[A\subseteq\{0,1\}^\ast\in P:\] \[\exists M\in\text{polynomial time TM}. \forall x\in\{0,1\}^\ast. x\in A\iff M(x)=1\]

NP问题

对于该问题的所有输入，无法保证在多项式时间内一定能得到结果，但可以在多项式时间内完成对某一结果的验证。从语言的的角度，使用非确定性图灵机(NTM)(即每一次状态的迁移由输入以及一比特随机数决定)可做如下定义

\[A\subseteq\{0,1\}^\ast\in NP:\] \[\exists M\in\text{polynomial time NTM}. \forall x\in\{0,1\}^\ast. x\in A\iff\exists r\in\{0,1\}^{p(\vert x\vert)}.M(x,r)=1\]

此外如果将定义中使用的NTM视为一个属于$P$的语言，则可改写定义为如下形式

\[A\subseteq\{0,1\}^\ast\in NP:\] \[\exists B\in P. \forall x\in\{0,1\}^\ast. x\in A\iff\exists r\in\{0,1\}^{p(\vert x\vert)}.(x,r)\in B\]

coNP问题

从语言的角度来讲，coNP问题属于NP问题的补集，即

\[A\subseteq\{0,1\}^\ast\in coNP\iff \{0,1\}^\ast\backslash A\in NP\]

仿照NP的定义，完整形式可写为

\[A\subseteq\{0,1\}^\ast\in coNP:\] \[\exists B\in P. \forall x\in\{0,1\}^\ast. x\in A\iff{\color{red}\forall}r\in\{0,1\}^{p(\vert x\vert)}.(x,r)\not\in B\]

若将B的补集重新命名为B，则可将不属于改写为属于，使得coNP与NP的定义只有量化子不同，即

\[A\subseteq\{0,1\}^\ast\in coNP:\] \[\exists B\in P. \forall x\in\{0,1\}^\ast. x\in A\iff\forall r\in\{0,1\}^{p(\vert x\vert)}.(x,r){\color{red}\in}B\]

Polynomial Hierarchy

在以上的定义过程中，借由P的定义，使得NP以及coNP的定义不在依存于某一特定多项式时间机器，仅由命题的量化子$\exists$和$\forall$加以区别。将此种定义方式泛化后则可做如下定义

\[\Gamma=\{0,1\}^{p(\vert x\vert)},A\subseteq\{0,1\}^\ast\in\Sigma_k^P:\] \[\exists B\in P. \forall x\in\{0,1\}^\ast.x\in A\iff {\color{red}\exists}r_k\in\Gamma. {\color{red}\forall}r_{k-1}\in\Gamma. \dots ?r_1\in\Gamma. (x,r_k,\dots,r_1)\in B\]

其中存在量化子和全称量化子交替出现，即如果k为偶数$?=\forall$，k为奇数$?=\exists$。那么，与$\Sigma_k^p$相对的其补集$\Pi_k^p$可以根据命题逻辑做如下定义

\[\Gamma=\{0,1\}^{p(\vert x\vert)},A\subseteq\{0,1\}^\ast\in\Pi_k^P:\] \[\exists B\in P. \forall x\in\{0,1\}^\ast.x\in A\iff {\color{red}\forall} r_k\in\Gamma. {\color{red}\exists} r_{k-1}\in\Gamma. \dots ?r_1\in\Gamma. (x,r_k,\dots,r_1)\in B\]

如此一来，P、NP以及coNP则可划入统一定义内了。

  • $P=\Sigma_0^p=\Pi_0^p$
  • $NP=\Sigma_1^p$
  • $coNp=\Pi_1^p$

最后将所有的$\Sigma_k^P$统称为多项式谱系PH。

\[PH=\bigcup_{k\in N}\Sigma_k^P\]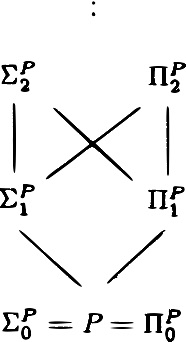

Collapse

当给出适当的假定，那么多项式谱系就会出现坍缩的现象，即某一层级以上的问题均等价。常见的假定有

  • $P=NP\implies PH=P$
  • $NP=coNP\implies PH=NP$

将这两个命题推广后可得

  • $\Sigma_k^P=\Sigma_{k+1}^P\implies PH=\Sigma_k^P$
  • $\Sigma_k^P=\Pi_k^P\implies PH=\Sigma_k^P$

在此简单证明推广后的第一个命题。

  • Step1: prove $\Sigma_k^P=\Pi_k^P$
\[\text{we have }\Pi_k^P\subseteq\Sigma_{k+1}^P=\Sigma_k^P\text{ then}\] \[\begin{aligned} L\in\Sigma_k^P\implies &\bar{L}\in\Pi_k^P\subseteq\Sigma_k^P\\\implies &\bar{\bar{L}}=L\in\Pi_k^P\\\implies &\Sigma_k^P\subseteq\Pi_k^P\\\implies &\Sigma_k^P=\Pi_k^P \end{aligned}\]
  • Step2: prove $\Sigma_i^P,\Pi_i^P\subseteq\Sigma_k^P=\Pi_k^P\implies\Sigma_{i+1}^P,\Pi_{i+1}^P\subseteq\Sigma_k^P=\Pi_k^P$ by induction
\[\begin{cases} L\in\Sigma_{i+1}^P\xlongequal{\text{by definition}} \exists r.\Pi_i^P= \exists r.\Sigma_k^P\xlongequal{\text{by combining the first 2 }\exists} \Sigma_k^P\\ L\in\Pi_{i+1}^P\xlongequal{\text{by definition}} \forall r.\Sigma_i^P= \forall r.\Pi_k^P\xlongequal{\text{by combining the first 2 }\forall} \Pi_k^P=\Sigma_k^P \end{cases}\]
  • Step3: now $\Sigma_k^P=\Sigma_{k+1}^P=\Sigma_{k+2}^P=\dots$ holds, then there is $PH=\bigcup_{i\in N}\Sigma_i^P=\Sigma_k^P$